PCB 'Boat' with led lights

During a recent event i did see this DIY kit for small boat.
It is intended for water scouts, however i  could not resist to buy it as it looks very nice and costs only a few euro's.
I did not opened the package or assembled it yet, so this is more like an 'Mailbag' object, that i did not got via mail. However if you like it, it can be ordered over internet.
The (led) lights can be controlled with the two pushbuttons or by touching the metal contacts near the helm with wet fingers.

https://kitbuilding.org/index.php?option=com_virtuemart&view=productdetails&virtuemart_product_id=114&virtuemart_category_id=24&lang=nl

Using IPX connectors

For my VNA i have a RF demo kit using IPX connectors. I wanted to see how easy or difficult it is to use this small IPX connectors for my own projects, so i ordered some and also some PCBs at JLCPCB 

The first connector i soldered was a failure. Measuring with my ohm meter gave a short circuit. However the next attempts went a lot better. I first tinned the connection pad with alsomost no solder. After that i placed the connector. Heated up the connections and the solder joints were made. Measuring showed they where electrical oke. I got very optimistic and almost was convinced that everything was going more easy than expected.
The only real problem that i did see at that moment was the orientation of the connector. When looking on the top of my (probably to cheap) connector there are 2 possibible orientations that i could not distinguish. And one of them is wrong. So the correct orientation of the connector looked the difficult point. For the rest it was going much more easy than expected. 

Using the connectors showed the real problem. On the RF demo board i had no problem connecting and disconnecting IPX cables. However using my own soldered connectors gave problems when trying to  disconnect the cable. The connector would not detach easy and in some occasion the connector sticked to the cable while detaching from the PCB.

Removing the connector from the cable without the PCB was even more problematic. A part of the connector did stay in the cable part.

I will continue with some experiments using the IPX connectors (that are also a lot cheaper than the SMA connectors,
Perhaps my soldering skills will improve to avoid damaging cables with IPX plugs. However i expect i will more use the SMA connectors and also order more SMA connectors and some additional SMA to IPX cables.

   

Mailbag - September 2022

 My Mailbag from China of September 2022
 ( 04OCT2022 published on my blog)

Some more of this nice and  cheap cases for my glasses.  I already did buy  some however with sun glasses and computer  glasses i needed some  more, also for my family.

PCB antenna

SMA Cables

PCB to play with RF experimenting for my VNA.  Before using it i need to so some soldering (and also make some additonal Dupont pins with through, open and 50 ohm load to do calibration and use for wiring. Probably i will make a separate blog post about this experimenting board.

SMA Cables with crocodile clips

Some SMA chassis connectors

Banana - Dupont cables

Received some Banana plugs

and created some cables with Dupont connectors 

What i don't like at the banana plugs that i received is the lack contrast between the black and blue plugs.

Audio transformer - breadboard friendly

Some time ago i ordered some cheap 600:600 ohm audio transformers to use them for some experiments. To easy wiring up an experiment it is possible to plug a transformer direct in a breadboard. The audio transformers fit exactly in a 3*4 grid on a breadboard. (With normal mains transformers I would not recommend this as i don't think it is safe to use high voltages or mains on a breadboard.)
I liked to make a more breadboard friendly version to handle the little transformer more easy, make it easy to move the transformer to other places on the breadboard and have the connections always at the same distances and also get somewhat more robust pins.

 A special PCB for the transformer could have been created, however i still had some 8 pin SMD PCBs and i realized they can be easy adapted for this transformers. This are small PCBs, normally used for 8 pin SMD ICs to making through hole compatible (or make them usable on a breadboard).

At the copper connections for the 8 pin SMD IC some connections were made:  pin 1 to 2 , 3 to 4 , 5 to 6 and 7 to 8. A small wire with some solder to bridge the gaps was used as solder alone tended to flow back on the pads. When you want a connection it sometimes does not work and when you don't want a connection.... 

The wires of the audio transformer fit exactly as 3*4 grid in pin holes 2, 4, 5, and 7. However first the Dupont male pins at pin 1, 8, 3 and 6 (see photos) were soldered as soldering the transformer first would make it more difficult.
For stability 2 strips with 4 male Dupont pins were used, first removing the middle 2 pins as they are not needed.  

1	2	3	4
8	7	6	5

The green positions are wires for the audio transformer and at the red positions are for the Dupont pins.  As there are connections between pin 1-2 , 3-4 , 5-6 and 7-8 the transformer is now breadboard friendly.

(Picture with breadboard, a breadboard friendly and a direct plugged in audio transformer and some other components)

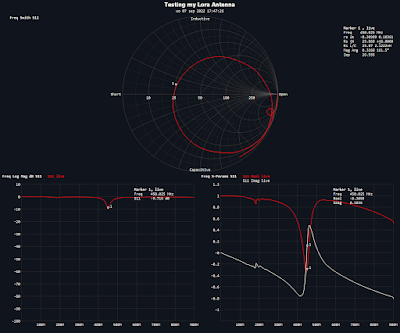
Vector Network Analyzer ( VNA) - 4 - Testing a 'Lora' antenna

With my Vector Network Analyzer i decided to test a LoRa antenna that i had still in a part box as i was never successful in using it.
In my region the Frequency for Lora is 868MHz (and so is my Lora hardware).
However using  my VNA i found out relative easy that this antenna would be more successful in the 433 MHz region and would not be very useful at 868 MHz ! 

 

This explained why i never had any good results using this antenna !

I expect this antenna was listed a LoRa antenna when i did buy it, however not for my region.

Non sequential computing environment and Forth -2-

In part -1- of this series this table was presented to to show some Forth words.
The header part of the table is in bold.

Table 1

	TOS	n1	n2	n3
SWAP	TOS	n2	n1	n3
DROP	TOS - 1		n2	n3
+	TOS - 1		n1 + n2	n3

This table is not (yet) a real Forth table and also can be simplified.
Calculations in this table are 'normal algebra' and not in Forth RPN calculations.
'Normal algebra' n1 + n2 becomes in RPN  n1 n2 + 
As already mentioned in my previous post the change of TOS depends on the amount of bits. The TOS should perhaps should be decremented by 2 or another value depending on the amount of bits in each stack item and the memory width.  It is a system constant depending on the implementation.
In this article series i will use SWDTH (stack width). In the RPN table  TOS - 1 should be written as TOS  SWDTH -

Table 2

	TOS	n1	n2	n3
SWAP	TOS	n2	n1	n3
DROP	TOS SWDTH -		n2	n3
+	TOS SWDTH -		n1 n2 +	n3

Some things in this table are still confusing (however it looks already more Forth).
For example a 'strange historical convention' of n1 n2 n3 where
n1 is the item on top of the stack,  n2 is the item just below it and n3 is two steps below. Another way is to see n1 n2 n3 as memory locations where values calculated are stored.  n1 is TOS @ and n2 is TOS SWDTH - @

Table 3

	TOS	n1	n2	n3
	TOS	TOS @	TOS SWDTH - @	TOS SWDTH 2* - @
SWAP	TOS	n2	n1	n3
DROP	TOS SWDTH -		n2	n3
+	TOS SWDTH -		n1 n2 +	n3

In a real 'physical' implementation of the table it would be needed to include items above the TOS (Top Of the Stack) in case items are added or pushed to the stack. Also it would be strange to represent the first items above the stack using n0 . It would be more systematic if the item on top of stack was referenced as n0 and use n+1 and n-1 for the items just above or below. However in Forth for many years items on the stack where called n1 n2 n3 and breaking with this convention would cause a lot of confusion. Also we do not want tot use complicated difficult to read terms as TOS @ or TOS SWDTH - @  So i decided (temporary) to use p0 and not n1 see tabel below.

Table 4

	TOS	( n0 ? )	n1	n2	n3
	TOS	p1	p0	p-1	p-2
	TOS	TOS SWDTH + @	TOS @	TOS SWDTH - @	TOS SWDTH 2* - @
SWAP	TOS		n2	n1	n3
DROP	TOS SWDTH -			n2	n3
+	TOS SWDTH -			n1 n2 +	n3

In the next evolution of the table i added an example of a Forth word that pushes a value to the stack.
It is the Forth word 0 . It is a number implemented in this Forth table where the value 0 is pushed to the stack.
In the table header a new Forth word PA is introduced ( shorthand for ParameterStackAddress ).
The location is described using Forth word  PA to avoid using n1 n2 n3 or p0 p1 p2 notations, 

 : PA SWDTH * TOS @ + ;

Table 5

	TOS	( n0 ? )	n1	n2	n3
		p1	p0	p-1	p-2
Location	TOS	1 PA	0 PA	-1 PA	-2 PA
	TOS	TOS SWDTH + @	TOS @	TOS SWDTH - @	TOS SWDTH 2* - @
SWAP	TOS		n2	n1	n3
DROP	TOS SWDTH -			n2	n3
+	TOS SWDTH -			n1 n2 +	n3
0	TOS SWDTH +	0	n1	n2	n3

We now have almost everything described in Forth and RPN
To evolve the table further we need to do something with the gaps (empty spaces).

In fact there are several options to handle these gaps.
A) Handle a gap as something that not needs to be changed  ( "Ignore" or "don't change" )

Table 6a

	TOS	( n0 ? )	n1	n2	n3
		p1	p0	p-1	p-2
Location	TOS	1 PA	0 PA	-1 PA	-2 PA
	TOS	TOS SWDTH + @	TOS @	TOS SWDTH - @	TOS SWDTH 2* - @
SWAP	TOS	Ignore	n2	n1	Ignore
DROP	TOS SWDTH -	Ignore	Ignore	Ignore	Ignore
+	TOS SWDTH -	Ignore	Ignore	n1 n2 +	Ignore
0	TOS SWDTH +	0	Ignore	Ignore	Ignore

B) Fill gap with a "Null" value
"Null" is a special marker and keyword indicating that something has no value (in SQL )
Using  option 2 ( Null) the small table the table would look as below.

Table 6b

	TOS	( n0 ? )	n1	n2	n3
		p1	p0	p-1	p-2
	TOS	1 PA	0 PA	-1 PA	-2 PA
	TOS	TOS SWDTH + @	TOS @	TOS SWDTH - @	TOS SWDTH 2* - @
SWAP	TOS	Null	n2	n1	n3
DROP	TOS SWDTH -	Null	Null	n2	n3
+	TOS SWDTH -	Null	Null	n1 n2 +	n3
0	TOS SWDTH +	0	n1	n2	n3

Both representations have advantages and disadvantages.
I like option B) using Null as this removes garbage (data that is no longer needed) from the system. Keeping items in a system that are no longer needed can introduce errors and vulnerabilities,

C) A third option could be using Null and, when no changes are needed use some kind of Noop  (no operation, do nothing) indicator.

Table 6c

	TOS	( n0 ? )	n1	n2	n3
		p1	p0	p-1	p-2
	TOS	1 PA	0 PA	-1 PA	-2 PA
	TOS	TOS SWDTH + @	TOS @	TOS SWDTH - @	TOS SWDTH 2* - @
SWAP	Noop	Null	n2	n1	Noop
DROP	TOS SWDTH -	Null	Null	Noop	Noop
+	TOS SWDTH -	Null	Null	n1 n2 +	Noop
0	TOS SWDTH +	0	Noop	Noop	Noop

If Null and Noop are Forth words a table can be created that describes Forth words in Forth code. The Noop has as disadvantage that just rewriting the old value perhaps is as fast or even faster then  evaluating that something is a Noop and not changing a value.

Table 7

	TOS	( n0 ? )	n1	n2	n3
		p1	p0	p-1	p-2
	TOS	1 PA	0 PA	-1 PA	-2 PA
	TOS	TOS SWDTH + @	TOS @	TOS SWDTH - @	TOS SWDTH 2* - @
SWAP	Noop	Null	-1 PA	0 PA	Noop
DROP	TOS SWDTH -	Null	Null	Noop	Noop
+	TOS SWDTH -	Null	Null	0 PA -1 PA +	Noop
0	TOS SWDTH +	0	Noop	Noop	Noop

Extending the table with more Forth words gives the next table (Table 8)

Table 8

	TOS	( n0 ? )	n1	n2	n3
		p1	p0	p-1	p-2
	TOS	1 PA	0 PA	-1 PA	-2 PA
	TOS	TOS SWDTH + @	TOS @	TOS SWDTH - @	TOS SWDTH 2* - @
SWAP	Noop	Null	-1 PA	0 PA	Noop
DROP	TOS SWDTH -	Null	Null	Noop	Noop
+	TOS SWDTH -	Null	Null	0 PA -1 PA +	Noop
0	TOS SWDTH +	0	Noop	Noop	Noop
1	TOS SWDTH +	1	Noop	Noop	Noop
2	TOS SWDTH +	2	Noop	Noop	Noop
3	TOS SWDTH +	3	Noop	Noop	Noop
4	TOS SWDTH +	4	Noop	Noop	Noop
-1	TOS SWDTH +	-1	Noop	Noop	Noop
-2	TOS SWDTH +	-2	Noop	Noop	Noop
Noop	Noop	Noop	Noop	Noop	Noop
-	TOS SWDTH -	Null	Null	0 PA -1 PA -	Noop
*	TOS SWDTH -	Null	Null	0 PA -1 PA *	Noop
/	TOS SWDTH -	Null	Null	0 PA -1 PA /	Noop
=	TOS SWDTH -	Null	Null	0 PA -1 PA =	Noop
@	Noop	Null	@	Noop	Noop
!	TOS SWDTH -	Null	Null	Null	Noop
2*	Noop	Null	2 *	Noop	Noop
2*	Noop	Null	2*	Noop	Noop
TOS	TOS SWDTH +	TOS	Noop	Noop	Noop
TOS	TOS SWDTH +	"Value"	Noop	Noop	Noop
SWDTH	TOS SWDTH +	"Value"	Noop	Noop	Noop
SWDTH+	Noop	Null	Noop	Noop	Noop
SWDTH-	Noop	Null	Noop	Noop	Noop

In the last part of table 8 some issues can be seen that need (and can) be solved.  Therefor i did write it in Italics and some words i described in multiple ways.

! Can't be full described in this table.The result of ! will be that 2 items are removed from the stack. An address and a value. The value will be stored at the address. However it is not easy to extend the lookup table so it will include all addresses in memory. ( @ can be described in the table. However there must be some kind of low level implementation!)

2* multiplies the value that is on top of stack by two. It can be described as just doing 2 *
Written in Forth code : 2* 2 * ;  
However in some Forth systems this is implemented in low level code as it can be executed fast,  This is just one example, however in general this creates a dilemma when trying to make a table like this. Many Forth words can easy be defined as itself, However that does not explain what these Forth words do. Also sometimes these words can be implemented in another way using other Forth words or should  call low level code.  

TOS ( Top Of Stack) is a variable. It it can be put in the table just calling some implementation of itself. However an easy implementation is pushing 'the value of the address' on the stack.

 SWDTH is a (system) constant, as described in the beginning of this article. A constant can be described in this table as it self, Or just put the value on the stack comparable to TOS

Some sequences of operations appear very often in this table. Examples are
TOS SWDTH + and TOS SWDTH + and also my new Forth word PA
  : PA SWDTH * TOS @ + ;
This indicates that speeding up these sequences can speed up the Forth system. 

We have seen that we can put the descriptions of (several) Forth words in a table.
Can that help us in a new Forth implementation and what about a 'Non sequential computing environment'? Yes, if we can describe Forth words in a table we can describe Forth in a table. This not only makes Forth portable, it also makes it possible we can create Forth in a table environment, e.g. a relational database.

P0cForth

What is P0cForth?

P0cForth is NOT another (full) Forth implementation. It is a only minimalistic Forth like system and my idea about P0cForth, I respect other ideas about minimalistic Forth and even opinion that this is so minimal that it is not a real Forth system. That is why it has a 0 in it name.

Why P0cForth?

For a long time I was thinking what Forth words are minimal needed to code to create a Forth (like) system. There are guides what Forth primitives need to be created to bootstrap a full Forth system. However I wanted a minimalist set of Forth words. Not to bootstrap a Forth system, only as a proof of concept for a Forth system that can be extended. A search on internet gives information about several interesting minimal Forth systems. Even systems minimal systems including @ ! however that is not what i wanted.
Also wanted to give it a name. I decided for P0cForth , "Proof of concept Forth" , i changed the o to 0.
It is to have bare minimal system that is relative easy to build (and can be extended) to have a proof of concept Forth system. 

What words/code need to be in P0cForth?

In the Forth2020 Zoom meeting on 9 januari 2021 Dr Ting talked about  Jeforth 2.01.
He mentioned a minimal system with 9 Forth words
: ; * . , dup dolit ret here
He also presented simple demos:
: square dup * ;
: quad square square ;
; octet quad quad ;
8 octet . 4 octet .

I used this 9 words as a start for P0cForth., However, I want to

reduce it even more.

So I ended up with this 5 words:
: ; * . dup 
I decided to reduce the system even more by omitting the interpretation of numbers defining (some) numbers direct as words. This would decrease the programming code and logic. And yes when extending the proof of concept Forth real handling of numbers would be useful and literals and dolit can be very useful. However I wanted to reduce it as much as possible. Literals are a very useful method of implementation, however i did not want to force this as a solution for handling numbers in my definition of P0cForth.
The code created for a number as a Forth words for a target system can be easy copied and adapted for another number. So it could be easy extended to include a lot of other numbers. However i wanted it to  as minimal as possible.

What numbers would be needed  minimal to have a proof of concept Forth system? At first did think at a minimum i would be needing the numbers 0 1 2 3 and (perhaps) -1 With this numbers you can play in the minimal PocForth for testing. And these numbers could be included in the dictionary.
With * and -1 it can be  and easy extend it to numbers in the range -4 to 4 (However if you continue reading to the end you will see this idea was wrong. Only one very special number is sufficient to create all numbers!)

: 4 2 2 * ;
: -2 -1 2 * ;
: -3 -1 3 * ;
: -4 -1 4 * ;
Also the demo mentioned above can be tested (after creating 8)

: 8 4 2 * ;

: square dup * ;
: quad square square ;
; octet quad quad ;
8 octet . 4 octet .

Adding code for a + function would make it possible to extend the number range even further without having gaps.

My first idea of a minimal P0cForth that could be a first start for a minimal Forth as

5 Forth words                 : ; * . dup
5 ‘number words’           -1 0 1 2 3

Creating e.g. a text input stream processor with this 6 different type of words would give a proof of concept system that could be used as a basis to create a full Forth system. 

Two facts made me not complete happy with this set of words.
- The possibility to build a complete Forth with these words is missing. it is only possible to extend this Forth by changing the 'external' code and add more words. However this minimal words can be a good basis of a proof of concept when creating a new Forth.

- And most important I did think it would be possible to reduce this word set even more!

So i started to reducing
1 is not needed as it could be defined by the other words
: 1 -1 dup * ;

If i would add the Forth word + 2 and 3 can be removed 
: 2 1 dup + ;

: 3 1 dup dup + + ;

Also 0 is not needed as it can be created

: 0 -1 1 + ; 

: 0 -1 dup dup * + ;

I would never have imagined that it was only needed to have one number to create other numbers, and that that number would be -1  

P0cForth minimal wordset 

No interpretation of numbers needed and only 7 words 

:  ;  .  *  dup  +  -1

Here some demo code to demonstrate what can be done with this 7 word system

: 0 -1 dup dup * + ;

: 1 -1 dup * ;

: 2 1 dup + ;

: 3 1 dup dup + + ;

: 4 2 dup * ;

: 8 4 2 * ;

: - -1 * + ;

: square dup * ;

: quad square square ;
: octet quad quad ;

3 square .
8 octet . 

4 octet .

8 3 - .

I think it is possible to reduce this 7 word set even more or add more capabilities adapting the selection of this words.
A simple option would be to reduce the word set would be omitting ; and have a the new definition, that in Forth starts with the colon :  close always at the end of the line.